|
NAZIV KOLEGIJA: Seminar 2 - Odabrane teme iz geometrije |
||
|
CILJ KOLEGIJA: Cilj seminara je studente/ice putem odabranih tema osposobiti za samostalan i projektni (timski) rad: istraživanje, pronalaženje i pretraživanje literature (na svim dostupnim medijima – tiskanim i elektroničkim, posebno na internetu, ali stručno i selektivno), pripremu seminarskog rada - eseja u pisanom obliku (uz pomoć računala) i usmeno izlaganje (prezentaciju) obrađene teme. Konkretno, studenti(ce) će se upoznati s odabranim temama (srednjo)školske geometrije koje se ne obrađuju detaljno u ostalim kolegijima a nužna su kompetencija učitelja/ice matematike u srednjoj školi. Teme studentskih projekata izabrane su tako da omogućuju osposobljavanje studenata/ica, budućih učitelja/ica matematike, za afirmaciju apstraktnog načina razmišljanja, matematičke preciznosti i analitičkog pristupa problemima kao temeljnih načela nastave matematike (posebno geometrije) na svim obrazovnim razinama. |
||
|
NASTAVNI SADRŽAJI: Seminar – Odabrane teme iz geometrije realizirat će se u obliku sustava projektne nastave, poštivanjem svih njenih etapa i zakonitosti. Svaki projektni tim bit će sastavljen od 3 studenta/ice, a projektni zadatak je obraditi zadanu temu te ju prezentirati u pismenom i usmenom obliku ostalim polaznicima/ama seminara. Bit će obrađene sljedeće teme: 1. Sferna geometrija. Osnovni pojmovi geometrije na sferi. Osna simetrija, rotacija, translacija, klizna simetrija i njihova svojstva. Segmenti, zrake, kutovi. Sferni trokut i osnovne veze među elementima sfernog trokuta. Pravokutni sferni trokut. Površina, paralelni pomak i Gauss-Bonnetova formula. Primjene sferne trigonometrije. 2. Poligoni. Osnovni pojmovi. Konstruktibilnost pravilnih poligona. Gaussov teorem. Konstrukcije i metode približnog crtanja poligona. 3. Osobite točke trokuta. Četiri karakteristične točke trokuta. Druge osobite točke trokuta i pridružene figure: izogonalne točke, Brocardova, Lemoinova, Gergonneova, Nagelove, Tarryeva i druge. 4. Kružnice i trokuti. Razne kružnice vezane uz trokut: opisana, upisana, pripisane, Tuckerove, Lemoineove, Taylorova, Feuerbachova i dr. Planimetrijske tvrdnje koje opisuju odnose trokuta i pridruženih mu kružnica. Rad će se odvijati u ovim etapama: 1. Formiranje studentskih projektnih timova i odabir projektnih tema. (1 tjedan) 2. Rad na projektima. (3 tjedna) Svaki projektni tim samostalno radi na realizaciji projekta (istražuje, pretražuje literaturu, pronalazi i selektira informacije, priprema seminar u pisanom obliku te priprema javnu prezentaciju teme). U terminima nastave održavat će se sastanci projektnih timova i nastavnika – nositelja kolegija, na kojima će timovi informirati o toku rada na projektu, a nastavnik (menadžer svih projekata) ih usmjeravati i pomagati im. 3. Javna prezentacija projektnih tema. (11 tjedana) Svaki projektni tim predstavit će rezultate svog istraživanja ostalim polaznicima/ama seminara. |
||
|
OBAVEZNA LITERATURA: 1. B. Pavković, D. Veljan, Elementarna matematika 1, Školska knjiga, Zagreb, 2003. 2. B. Pavković, D. Veljan, Elementarna matematika 2, Školska knjiga, Zagreb, 1995. |
||
|
DOPUNSKA LITERATURA: 1. D. Palman, Trokut i kružnica, Element, Zagreb, 1994. 2. P. J. Ryan, Euclidean and non-Euclidean geometry, Cambridge University Press, London, 1995. 3. D. W. Henderson, Experiencing geometry on plane and sphere, Prentice Hall, Upper Saddle River, NJ, 1996. |
- Nositelj kolegija: Maja Resman
- Nositelj kolegija: Ilja Gogić
Kolegij se održava u ljetnom semestru, a nastava se sastoji od dva sata predavanja i dva sata vježbi svakog tjedna.
Cilj kolegija je sistematizirati, produbiti i proširiti znanje studenata o vektorima, planimetriji i analitičkoj geometriji ravnine te upoznati studente s analitičkom geometrijom prostora. Očekujemo da će nakon upoznavanja s vektorima i osnovnim elementima analitičke geometrije studentima biti olakšano proučavanje matematičkih struktura koje se temelje na ovim pojmovima.
- Nositelj kolegija: Zvonimir Bujanović
- Nositelj kolegija: Boris Muha
- Izvođač kolegija: Barbara Bošnjak
- Izvođač kolegija: Matea Čelar
- Izvođač kolegija: Lucija Validžić
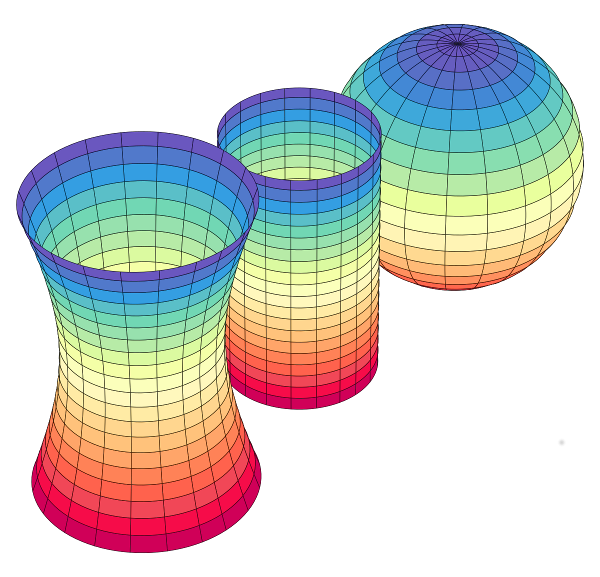
Kolegij Uvod u diferencijalnu geometriju je jednosemestralni izborni kolegij koji se izvodi na Matematičkom odsjeku u ljetnom semestru. Obrađuje temeljne koncepte klasične diferencijalne geometrije krivulja i ploha u prostoru.
- Nositelj kolegija: Željka Milin Šipuš
- Izvođač kolegija: Domagoj Lacmanović
- Izvođač kolegija: Martina Stojić
- Izvođač kolegija: Lucija Validžić
- Newtonova mehanika. Gibanje. Newtonovi aksiomi. Momenti. Energija. Gibanje u relativnom sustavu referencije.
- Lagrangeova mehanika. Varijacijski račun. Lagrangeove jednadžbe. Hamiltonove jednadžbe. Glatke mnogostrukosti.
- Gibanje krutog tijela. Tenzor inercije. Eulerove jednadžbe.
- Parcijalne diferencijalne jednadžbe. Jednadžbe i sustavi prvog reda. D'Alembertova formula za valnu jednadžbu u jednoj dimenziji. Poissonova formula za jednadžbu difuzije u jednoj dimenziji. Klasifikacija jednadžbi drugog reda. Separacija varijabli: valna jednadžba. Fourierovi redovi. Sturm - Liouvilleova zadaća. Laplaceova jednadžba.

- Nositelj kolegija: Marko Erceg
- Nositelj kolegija: Marko Vrdoljak
- Izvođač kolegija: Marija Galić
- Izvođač kolegija: Petar Kunštek
Cilj kolegija je upoznati studente s osnovnim svojstvima ograničenih linearnih operatora na normiranim prostorima. Dokazat će se neki od klasičnih teorema funkcionalne analize: princip uniformne ograničenosti, teorem o otvorenom preslikavanju i teorem o zatvorenom grafu, te će se dati pregled osnovnih rezultata o spektru. Kolegij će dati i uvod u teoriju normiranih algebri.
- Nositelj kolegija: Damir Bakić
- Izvođač kolegija: Tomislav Berić
|
ILJ KOLEGIJA: Cilj seminara je studente/ice putem odabranih tema osposobiti za samostalan i projektni (suradničko – timski) rad: istraživanje, pronalaženje i pretraživanje literature (na svim dostupnim medijima – tiskanim i elektroničkim, posebno na internetu), pripremu seminarskog rada - eseja u pisanom obliku (uz pomoć računala) i usmeno izlaganje (prezentaciju) obrađene teme. Konkretno, studenti(ce) će se upoznati s odabranim temama iz područja informacijsko – komunikacijskih tehnologija koje se ne obrađuju detaljno u ostalim kolegijima a nužna su kompetencija učitelja/ice informatike u srednjoj školi. Teme studentskih projekata izabrane su tako da omogućuju osposobljavanje studenata/ica, budućih učitelja/ica informatike, za afirmaciju problemnosti i suvremenosti kao temeljnih načela nastave informatike na svim obrazovnim razinama. |
||
|
NASTAVNI SADRŽAJI: Seminar – Odabrane teme iz računarstva realizirat će se u obliku sustava projektne nastave, poštivanjem svih njenih etapa i zakonitosti. Svaki projektni tim bit će sastavljen od 3 studenta/ice, a projektni zadatak je obraditi zadanu temu te ju prezentirati u pismenom i usmenom obliku ostalim polaznicima/ama seminara. Rad će se odvijati u ovim etapama: 1. Formiranje studentskih projektnih timova i odabir projektnih tema. (1 tjedan) Studentima/cama će biti ponuđene sljedeće teme: Paradigme programiranja (naredbovna, objektno - orijentirana, funkcionalna, logička); Sigurnost računalnih sustava; Web tehnologije; Računalna grafika, Multimedijski sustavi. 2. Rad na projektima. (6 tjedna) Svaki projektni tim samostalno radi na realizaciji projekta (istražuje, pretražuje literaturu, pronalazi i selektira informacije, priprema seminar u pisanom obliku te priprema javnu prezentaciju teme). U terminima nastave održavat će se sastanci projektnih timova i nastavnika – nositelja kolegija, na kojima će timovi informirati o toku rada na projektu, a nastavnik (menadžer svih projekata) ih usmjeravati i pomagati im. 3. Javna prezentacija projektnih tema. (8 tjedana) Svaki projektni tim predstavit će rezultate svog istraživanja ostalim polaznicima/ama seminara. |
||
|
OBAVEZNA LITERATURA: 1. M. L. Scott, Programming language pragmatics, Morgan Kaufmann, 2000. 2. D. Gollmann, Computer Security, John Wiley & Sons, 1999. |
||
|
DOPUNSKA LITERATURA: 1. W. Stallings, Cryptography & Network Security: Principles & Practice, Prentice Hall, 2002. 2. J. D. Foley, A. Van Dam, S. K. Feiner, J. F. Hughes, Computer Graphics Principles and practice in C, 2nd edition, Addison Wesley, 1995. 3. Allan Watt, Alan Watt, 3D Computer Graphics, Addison-Wesley, 2000. 4. D. Hearn, M. P. Baker, Computer Graphics with Open GL, 3rd edition, Prentice-Hall, 2003. 5. R. Steinmetz, K. Nahrstedt, Multimedia: Computing, Communications and Applications, Prentice Hall Series in Innovative Technology, Prentice Hall, 1995. 6. N. Chapman, J. Chapman, Digital Multimedia, 2nd edition, John Wiley & Sons, 2004. 7. D. R. Stinson, Cryptography. Theory and Practice, CRC Press, 2002. 8. W. Stallings, Cryptography and Network Security. Principles and Practice, Prentice Hall, 1999. 9. D. Parker, Fighting Computer Crime – A New Framework for Protecting Information, John Wiley & Sons, 1998. 10. D. Dragičević, Kompjutorski kriminalitet i informacijski sustavi, Informator, Zagreb, 1999. |
- Nositelj kolegija: Goran Radunović
Cilj kolegija je studente upoznati s elementima teorije linearnih operatora na konačnodimenzionalnom vektorskom (unitarnom) prostoru.
- Nositelj kolegija: Ljiljana Arambašić
- Nositelj kolegija: Damir Bakić
- Izvođač kolegija: Tomislav Berić
- Izvođač kolegija: Ana Prlić
- Nositelj kolegija: Ilja Gogić
- Nositelj kolegija: Josip Tambača
- Izvođač kolegija: Matija Bašić
- Izvođač kolegija: Goran Radunović
Kolegij obrađuje osnove teorije holomorfnih funkcija jedne kompleksne varijable.

- Nositelj kolegija: Ljiljana Arambašić
- Nositelj kolegija: Pavle Pandžić
- Izvođač kolegija: Luka Cigler
- Izvođač kolegija: Ante Čeperić
- Izvođač kolegija: Mario Stipčić
- Izvođač kolegija: Martina Stojić
- Izvođač kolegija: Antonela Trbović
Ciljevi kolegija:
1. Usvojiti temeljna znanja o osnovnim sociološkim teorijskim pristupima i metodama analize obrazovanja, društvenim funkcijama i karakteristikama suvremenih obrazovnih sustava i njihovih mikrosocijalnih procesa.
2. Osposobiti studente za primjenu stečenih znanja kako bi razumjeli važnost društvenog konteksta i načine njegovog utjecaja na funkcioniranje i razvoj škole i nastavu kao konkretnu radnu sredinu učitelja/nastavnika.
Teme:
1. Predmet sociologije obrazovanja i pregled teorijsko-metodoloških pristupa (funkcionalizam, marksizam, socijalni interakcionizam, postmodernizam, itd.).
2. Društvene funkcije škole (socijalna integracija, profesionalna socijalizacija, kulturna transmisija, socijalna kontrola i selekcija, itd.).
3. Obrazovanje i reprodukcija društvenih nejednakosti (obrazovanje i socijalna struktura društva; obrazovanje, kulturni kapital i reprodukcija društvenih nejednakosti, itd.).
4. Jednakost i obrazovne šanse (žene, etničke zajednice, društveno marginalizirane grupe i jednakost obrazovnih šansi; nacionalne manjine i obrazovanje).
5. Škola kao organizacija i socijalni sustav, razred kao mikro socijalni sustav.
6. Društvo znanja, procesi globalizacije, promjene u obrazovanju.
7. Suvremeno društvo i promjene u nacionalnom kurikulumu (kurikulumske promjene u EU zemljama i Hrvatskoj).
8. Integracija Europe i obrazovni sustavi u Europi (stare i nove članice Europske unije).
9. Razvoj i struktura obrazovnog sustava u Hrvatskoj. (Pregled razvoja školskog sustava u kontekstu društvenih promjena u Hrvatskoj).
10. Globalizacija, europska integracija i promjene u obrazovnom sustavu u Hrvatskoj (Današnji obrazovni sustav u Hrvatskoj u kontekstu suvremenih društvenih i obrazovnih razvojnih trendova).
- Nositelj kolegija: Branislava Baranovic
- Nositelj kolegija: Eduard Marušić-Paloka
- Nositelj kolegija: Ivica Nakić
- Nositelj kolegija: Ivica Nakić
- Izvođač kolegija: Luka Cigler
- Izvođač kolegija: Matko Ljulj
Kolegij Osnove matematičke analize se održava u 4. (ljetnom) semestru na preddiplomskom sveučilišnom studiju Matematika; smjer:nastavnički, a sastoji se od četiri sata predavanja i dva sata vježbi tjedno.
U ovom se kolegiju proučavaju i teorijski strože formuliraju neki osnovni pojmovi na koje se nailazi u Diferencijalnom i integralnom računu 1 i 2. Uvodi se epsilon – delta terminologija i koristi za pedantno fundiranje pojmova te dokazivanje osnovnih teorema matematičke analize. Na predavanjima se uvode i obrađuju pojmovi te ilustriraju primjerima, dok na vježbama studenti usvajaju odgovarajuće tehnike pristupa pojedinim problemima i njihova rješavanja.
- Nositelj kolegija: Tomislav Berić
- Nositelj kolegija: Boris Guljaš
- Izvođač kolegija: Ana Bokšić
- Izvođač kolegija: Marko Radulović

- Nositelj kolegija: Mea Bombardelli
- Nositelj kolegija: Tomislav Pejković
- Izvođač kolegija: Ivan Krijan
- Izvođač kolegija: Martina Stojić
- Izvođač kolegija: Ivana Vukorepa
Ovo je napredni kolegij na doktorskom studiju računarstvo i matematika. Kolegij predstavlja moderne tehnike modeliranja i optimizaciji u podacima bogatom okruženju.
- Nositelj kolegija: Luka Grubišić
- Nositelj kolegija: Matija Bašić
- Nositelj kolegija: Željka Milin Šipuš
- Izvođač kolegija: Renata Vlahović Kruc
Kolegij na prvoj godini diplomskog studija Matematika i računarstvo
Nastava: Marko Horvat, predavanja i vježbe otprilike u omjeru 2:1
Gradivo:
1. dio semestra: teorija formalnih jezika (Chomskyjeva hijerarhija)
2. dio semestra: leksička, sintaksna i semantička analiza programskih jezika
- Nositelj kolegija: Marko Horvat
- Izvođač kolegija: Vedran Čačić
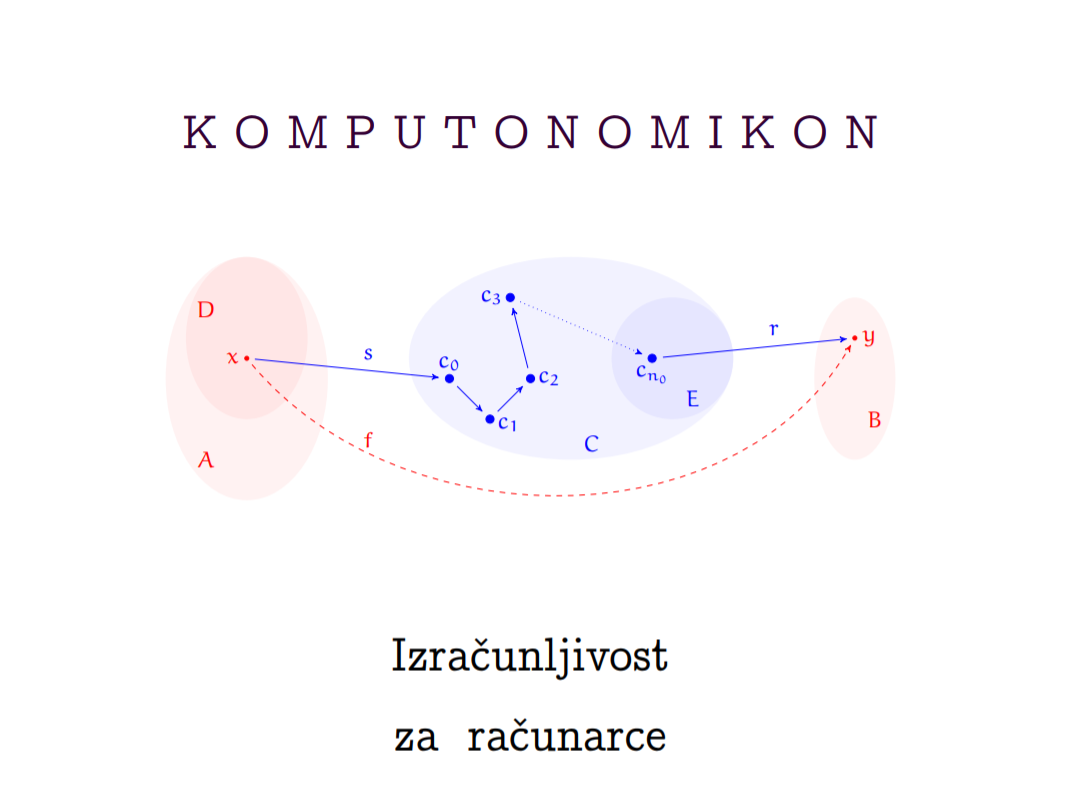
U prvom dijelu kolegija upoznajemo i analiziramo različite modele izračunavanja (RAM-stroj, Turingov stroj, parcijalno rekurzivne funkcije) te dokazujemo njihovu ekvivalentnost. Nativno proučavamo izračunljivost na prirodnim brojevima i nizovima znakova, razvijamo tehnike kodiranja kojima možemo proučavati izračunljivost nad ostalim domenama.
U drugom dijelu kolegija generaliziramo algoritamske sustave i uvodimo Church-Turingovu tezu, pomoću koje dokazujemo da su neki važni problemi neodlučivi. Razvijamo tehnike svođenja (redukcije) i aritmetizacije logike, kojima dokazujemo Churchov teorem o neodlučivosti logike prvog reda. Skiciramo dokaz Gödelovog prvog teorema nepotpunosti.
Dokazujemo velike teoreme teorije rekurzije (Kleenejev t. o normalnoj formi, t. o parametru, t. rekurzije, t. o fiksnoj točki, Riceov t., t. o selektoru, t. o grafu, t. enumeracije) te promatramo rekurzivno prebrojive skupove pomoću kojih formaliziramo paralelno računanje.
- Nositelj kolegija: Vedran Čačić
izborni kolegij na diplomskom studiju, smjerovi: * matematička statistika * računarstvo i matematika * nastavnički smjer matematika i informatika
nastava: Vedran Čačić, uglavnom vježbe, u praktikumu
Gradivo: dva velika ekosustava softvera kojim se često služe matematičari * Python (Anaconda): Jupyter, numpy, scipy, pandas, matplotlib, sympy * LaTeX (Overleaf): amsmath, thmtools, csquotes, KOMAScript, tikz, Beamer

- Nositelj kolegija: Vedran Čačić
Matematika, preddiplomski studij Molekularna biologija
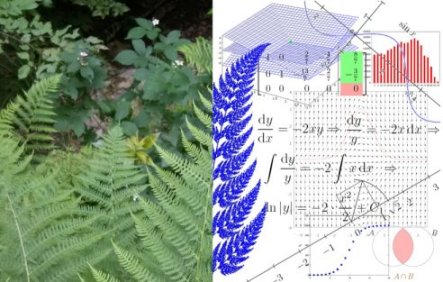
Cilj kolegija je upoznati osnovne pojmove diferencijalnog i integralnog računa (neprekidnost, limes, derivaciju, integral, obične diferencijalne jednadžbe) te osnovne pojmove i tehnike linearne algebre (vektore, matrice, Gaussovu metodu eliminacija, svojstvene vrijednosti). Na primjerima kao što su modeli rasta i modeli populacijske dinamike ilustrirat ćemo kako se ti matematički pojmovi i tehnike koriste za modeliranje procesa u prirodi.
- Nositelj kolegija: Vedran Krčadinac
CILJ KOLEGIJA: Upoznavanje s nekoliko naprednih tema iz područja relacijskih baza podataka, skladištima podataka, NoSQL paradigmom te smještajem i obradama velikih podataka (big data).
NASTAVNI SADRŽAJI:
1. Proširenja znanja o relacijskim bazama podataka. Složeni tipovi podataka. Distribuirane baze podataka. Ciljevi, svrha, prednosti i mane distribuiranja podataka. Struktura distribuirane baze, replikacija, fragmentacija. Protokoli za izvršavanje distribuiranih transakcija.
2. NoSQL paradigma. Razlozi nastanka. Agregatni model podataka. Svojstva NoSQL baza podataka. Konzistencija i CAP teorem. Vrste NoSQL baza podataka: ključ-vrijednost, dokumentske, grafovske i obitelj-stupaca baze podataka. Map/reduce algoritam u NoSQL bazama podataka.
3. Skladišta podataka (data warehouses). Ciljevi i svrha skladištenja podataka. Modeli skladišta podataka. Postupak modeliranja skladišta. OLAP. Postupak punjenja skladišta podataka (ETL).
4. Veliki podaci (big data). Distriburani datotečni sustavi. Google FS i HDFS. Apache Hadoop ekosustav. Map/reduce algoritam. Distribuirana izračunavanja i analize. Apache Spark.

- Nositelj kolegija: Ognjen Orel
Osnovni kolegij i numeričke matematike na doktorskom studiju. Pripremni kolegij za pristupni ispit.
- Nositelj kolegija: Luka Grubišić
Prvi dio kolegija Numeričko rješavanje parcijalnih diferencijalnih jednadžbi bavi se metodama konačnih diferencija i konačnih volumena primijenjenih na hiperboličke zakone sačuvanja te metodom konačnih elemenata za skalarnu eliptičku jednadžbu. Praktični dio kolegija sastoji se od programiranja u Dune biblioteci (www.dune-project.org).
- Nositelj kolegija: Mladen Jurak
- Nositelj kolegija: Mladen Jurak
- Nositelj kolegija: Anamarija Jazbec
- Nositelj kolegija: Tajana Ljubin Golub
- Izvođač kolegija: Ema Petričević
- Nositelj kolegija: Tajana Ljubin Golub
- Izvođač kolegija: Diana Olčar
